Malware analysts spend considerable time examining the conditions under which malicious programs will take certain actions. For example, consider a malware program that contains a check for the presence of a debugger, a common technique meant to hinder analysis. The analyst may wish to know if there is a viable execution path that circumvents this check and, if there is a path, what inputs and environmental conditions are needed to traverse it. We call this type of reasoning path finding. The paths to find can be based on numerous criteria, such as user-specified start and end addresses or passing through specific program points. CERT’s reverse engineers and malware analysts have found path finding is useful when analyzing malware.

In a previous post, we discussed Kaiju, the CERT/CC's extension framework to Ghidra, the National Security Agency’s software reverse engineering (SRE) tool suite. Kaiju includes many tools to support malware analysis and reverse engineering. One of the more complex plugins included in Kaiju is a Satisfiability Modulo Theories (SMT) based path analysis tool named GhiHorn. In this post I delve deeper into GhiHorn to discuss how it works and how it can be used to solve path analysis problems.

Path Finding Without Source Code

As noted above with the debugger detection example, we believe that many common challenges in malware analysis and reverse engineering can be framed in terms of finding a path to a specific point in a program. At the binary level we don’t have the extra information that you typically have in source code. For example, instead of programmer-named variables we must reason about CPU registers or memory values. Additionally, optimizations performed during compilation may result in exotic or convoluted code arrangements that make it hard to recognize common program features.

Recall the example from our previous blog post on binary path finding, which is shown in Figure 1. Finding a path from line 1 to the target at line 20 (marked as “Target line!”) is relatively straightforward by visual inspection: we know that local integer variable x must be set to 42 because of the condition at line 19, which can only happen at line 12 when variable y is equal to 2, which in turn depends on the three integer input parameters, i, j, and k being set to 6, 7, and 8, respectively.

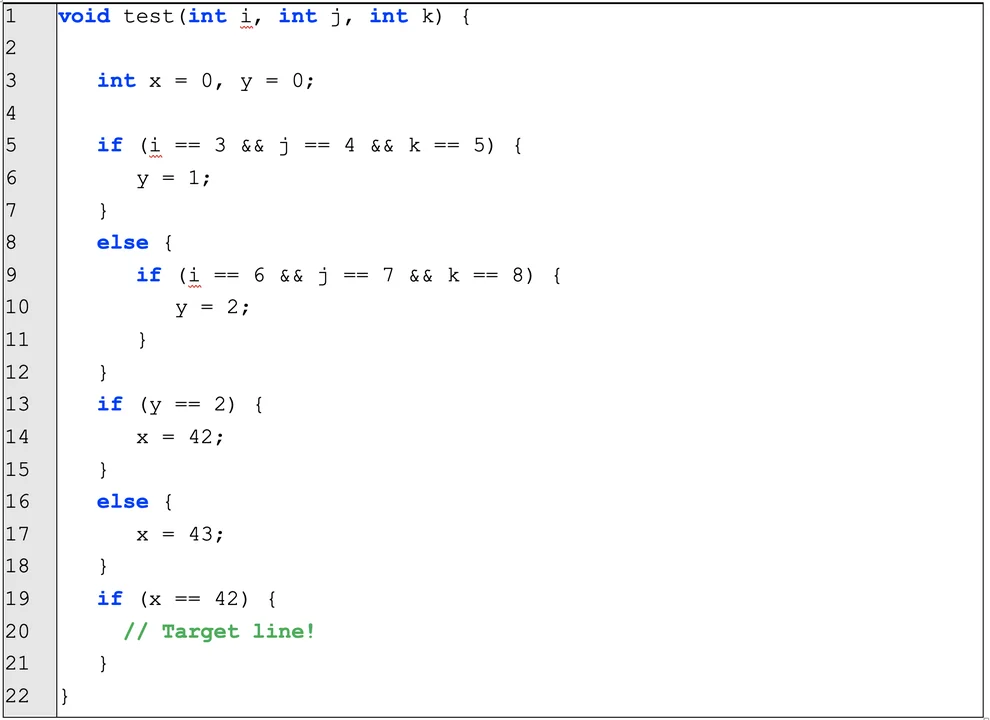
However, when this program is compiled, numerous complexities emerge:

• Variable names and types are lost.
• Optimizations may result in convoluted code structures.
• There are many assembly instructions that are combined to form higher-level operations.
• Each CPU provides its own instruction set architecture (ISA) with specific calling conventions, registers, and operations.

From Pharos to Ghidra

We have been developing tools to assess path viability in our Pharos Binary Analysis Framework for some time. Pharos’ path finding tools encode program control flow graphs as SMT assertions that are solved by the Z3 theorem prover. The original encoding scheme used in Pharos is based on mutually exclusive Z3 assertions that are generated using Pharos’ analysis. Representing a program using this scheme turned out to be cumbersome for several reasons:

• The notation was not designed for human legibility, e.g., data and control flow structures and the transitions between them were made using standard Z3 assertions, which made encoding control flow unnatural and hard for analysts to understand.
• Common program phenomena were challenging to model, such as calling functions, recursion, and complex data types.
• State variables became derived symbolic values generated by Pharos that could be hard to map back to meaningful program structures.

Our other Pharos-based path analysis tool is ApiAnalyzer. ApiAnalyzer traverses program control flow graphs looking for sequences of application program interface (API) function calls that match prescribed behavioral signatures. The problem of identifying a path in a program that satisfies specific constraints, such as traversing a sequence of API function calls, lends itself well to path finding. Our new work thus seeks to reframe this API analysis in terms of path finding.

The Pharos approach to program analysis was initially designed to be simple, fast, and useful for malware analysts. Many of these goals were achieved at the expense of deeper analyses. It turns out that advanced path analysis requires additional fidelity that Pharos had difficulty providing.

Pharos can answer certain questions quickly, for example: Is the value used at X the same as the value used at Y? Since Pharos focuses on speed, however, it trades off how complex paths can become before accuracy is no longer guaranteed. As a result, reasoning about complex program paths in Pharos is hard. As noted above, we were already exploring more rigorous path analysis using SMT solvers in Pharos when Ghidra was released. The Ghidra decompiler, with its rich programming API, opened new and exciting ways to approach path analysis problems.

GhiHorn

We have created a new Ghidra-based tool named GhiHorn (See Figure 2 below) to take advantage of our recent advances and to provide an extensible framework for binary-path analysis problems. GhiHorn helps reverse engineers and malware analysts answer interesting questions such as

• Does a path exist to a specified point in a program (i.e. feasibility)?
• If there is a path, what values should be assigned to program variables to reach it?
• If there is not a feasible path, why?
• Does the path indicate an interesting or indicative behavior?

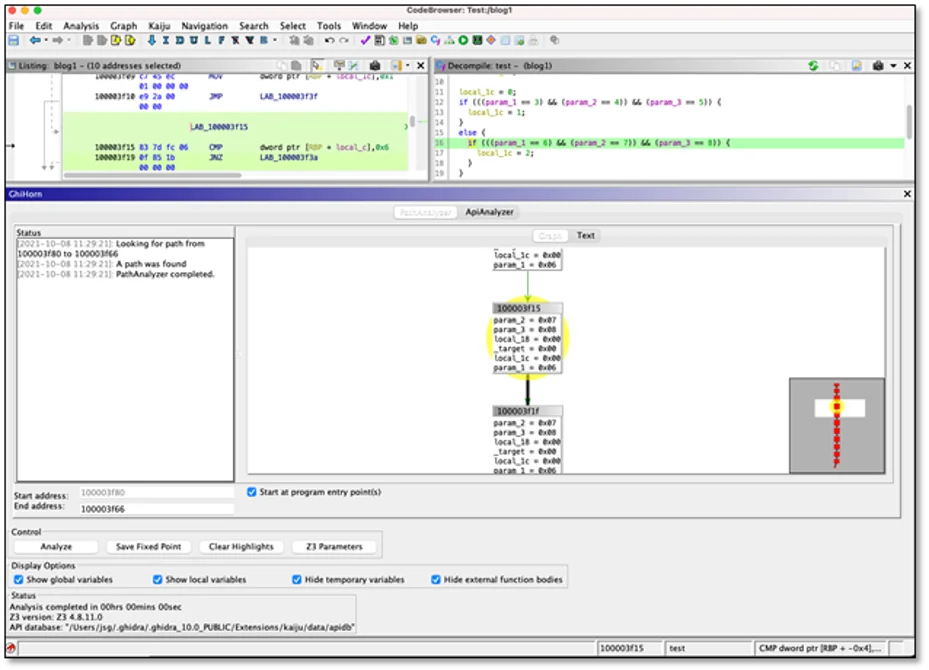
We've named this new Kaiju tool “GhiHorn” (GHI-dra HORN-ifier), in keeping with the tradition of similar source-code analysis tools using Horn clauses, including SeaHorn (a C language hornifier) and JayHorn (a Java hornifier). GhiHorn is created in the spirit of these other verification tools, but it operates on Ghidra-generated data structures, specifically p-code. Ghidra’s decompiler and p-code language provide robust information about program semantics for different architectures. According to Ghidra’s p-code documentation:

A p-code operation is the analog of a machine instruction. All p-code operations have the same basic format internally. They all take one or more varnodes as input and optionally produce a single output varnode.

Varnodes in Ghidra are data elements represented as triples (memory space, offset, and size) on which p-code operates. P-code and varnodes are critical to Ghidra’s decompilation process. Ghidra generates both p-code and varnodes for each instruction in a program during initial program analysis and disassembly. The p-code and varnodes initially generated are raw in the sense that they are only meant to represent the instruction semantics with little or no high-level information gleaned from higher order analysis.

During decompilation, pcode and varnodes are refined and associated with abstract local variables and source-code level data structures. We term this “high p-code” because it is bound to data structures in Ghidra that include decompilation information, such as HighVariables and HighFunctions. Fortunately, the structure of high p-code lends itself to SMT-based encoding.

With Ghidra providing the data and control flow structures necessary to represent a path, we need a way to encode the program structures for an SMT solver. Enter Horn clauses, which are a specific encoding for verification conditions that can be constructed automatically from program control flow structures. Researchers have continued to make advances in Horn clause solvers, and many SMT solvers, including Z3, now include Horn solvers, which makes Horn clause encoding a viable solution for path analysis problems. We delve into some of the details of how GhiHorn encodes p-code below.

GhiHorn Encoding

GhiHorn encodes Ghidra p-code as SMT-Lib Horn clauses suitable for the Z3 solver. Horn clauses are rule-like constraints expressed as implications. Horn clauses can represent transitions through a control flow graph of the logical form:

𝐼𝑛𝑝𝑢𝑡 𝐿𝑜𝑐𝑎𝑡𝑖𝑜𝑛 ∧𝐶𝑜𝑛𝑠𝑡𝑟𝑎𝑖𝑛𝑡𝑠⇒𝑂𝑢𝑡𝑝𝑢𝑡 𝐿𝑜𝑐𝑎𝑡𝑖𝑜𝑛Input Location ∧Constraints⇒Output Location

where an input location conjoined with constraints on state variables transitions to an output location. In program terms, the input location is the originating basic block, the constraints are conditions over program variables, and the output location is a succeeding basic block. An example of a conditional expression and the associated Horn rule generated for it are shown in Table 1 below. When control flow arrives at Line 1 and the variable x is 42, then control flow may progress to Line 2. Because this is a decision point in the code, a second rule is needed to transition from Line 1 to Line 3. Taken together, these rules model the conditional structure shown in the following source code.

Ghidra provides a control flow graph from which the input and output parts of the rules can be derived. Given that p-code represents machine instructions, you can use them to represent state transitions inside blocks. Translating p-code statements into Z3 expressions then turns out to be relatively straight forward. For example, here is a complex source code statement (shown in Table 2) that was generated by Ghidra’s decompiler: ((param_1 >> 2) + 1U & 0xff) == 0x55. This example is used because it decomposes to multiple p-code operations, and these can be mapped to Z3 expressions. Note that the source code operations, such as >> have analogs in both p-code (INT_SRIGHT) and in Z3 SMT (bvashr). For the most part variables are represented as 64-bit bit vectors.

Note that the varnodes present in p-code operations are replaced with variables in the final Z3 expression (e.g., param_1). This is possible because, during decomposition, Ghidra associates varnodes with higher-level decompiler elements, such as variables. Operating on meaningful data elements such as variables provides for much more interesting results, which are discussed below.

As the table above illustrates, the decompilation was generated by Ghidra. The p-code operations include varnodes represented as triples: (memory space, offset, size). The Z3 expressions are all equalities of the form output = operations input.

After each basic block is hornified it is arranged into a set of Z3 rules. Each rule is an implication where the antecedent is the source basic block and the consequence is the sink block. A complete example based on the Ghidra decompilation shown in Table 2 is shown in Figure 3. The rule captures the transition from the basic block at address 0x100003f60 to the basic block at address 0x100003fa2. The constraints capture conditions on param_1 taken from the p-code operations that must be true to enable the transition.

A collection of these rules is generated to represent a control flow graph for a program. Note that variables are passed as state (i.e., arguments) to both the input and output blocks. In this way, program state is updated and maintained. Ultimately the encoded program is passed to Z3, and GhiHorn queries for a state (i.e., the address present in the encoding) to determine if a viable path is present.

Although this approach to reasoning about program paths is intuitive it requires additional structures to model real programs. For simplicity’s sake, all memory operations are performed on a single large memory array (named Memory in Figure 3) that is managed by Z3. This approach keeps things simple but can be limited, and it is by no means performant. In future versions of GhiHorn we plan to improve memory modeling by better handling pointers and better representation of different memory regions.

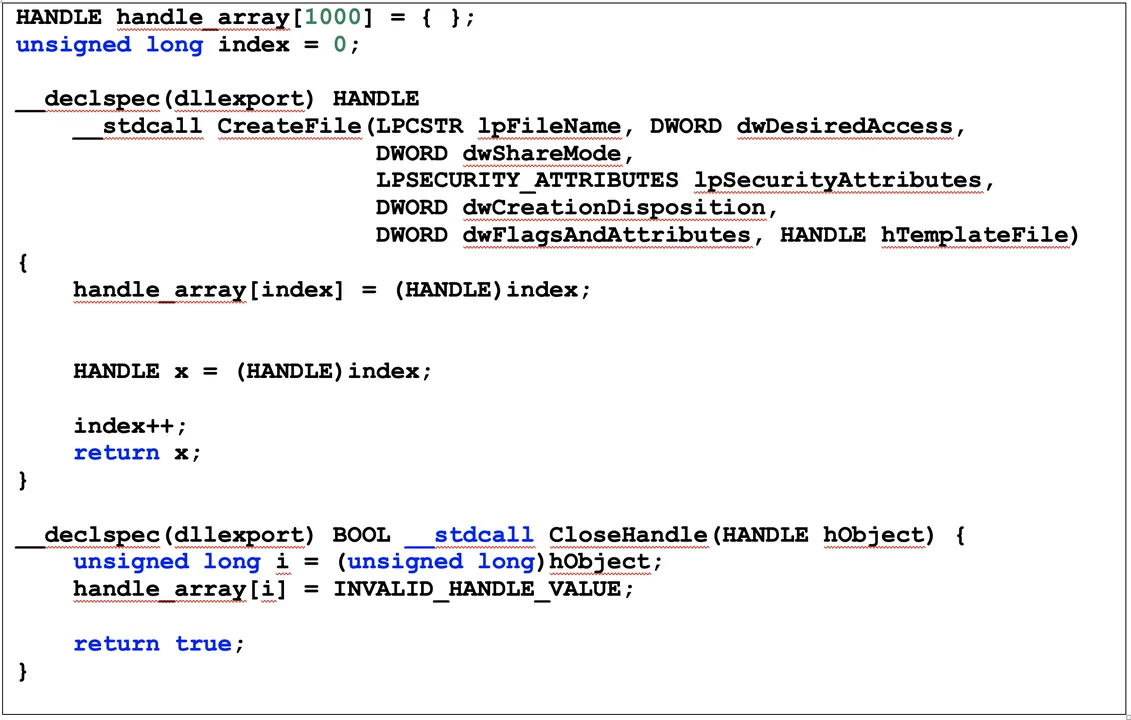
Another problem is how to handle external dependencies, such as imported API functions for which the code may not be available. GhiHorn provides a capability to build a simulated API ecosystem by compiling library files that contain simple implementations of common API functions. For example, Figure 4 shows the source code for the simulated API functions CreateFile() and CloseHandle(). In this example, the implementation simply maintains an array meant to model a file handle table, which makes it simple to track which handles are open and closed, nothing more.

Looking Ahead

In a future post I will present two path analysis tools that we have implemented on top of the Ghihorn platform: Path Analyzer and API Analyzer.