In a previous post, I discussed the Pharos Binary Analysis Framework and tools to support reverse engineering of binaries with a focus on malicious code analysis. Recall that Pharos is a framework created by our CERT team that builds upon the ROSE compiler infrastructure developed by Lawrence Livermore National Laboratory. ROSE provides a number of facilities for binary analysis including disassembly, control flow analysis, instruction semantics, and more. Pharos uses these features to automate common reverse engineering tasks.

Since our last post, we have developed new techniques and tools in the Pharos framework to solve a problem that may be of interest to reverse engineers and malware analysts. Specifically, this post describes how we have worked on techniques and tools to identify the specific program inputs and environments that are needed to reach an execution of interest to an analyst, which we call path finding.

We believe that finding paths in an executable can support various malware analysis activities. One area where path finding can be especially useful is bypassing run-time anti-analysis checks in the code. It is common for malware authors to include checks for various malware analysis tools and technologies, such as the presence of a debugger or execution within a virtual environment.

For example, newer versions of Poison Ivy and Upatre contain various anti-analysis techniques can detect if they are being analyzed and prematurely terminate themselves, thereby making certain types of malware analysis hard. Many of these techniques are well known but remain hard to cope with in practice. Analysts often must use specialized tools or manual binary editing to circumvent anti-analysis code, both of which can be complex and error prone. We believe that our new path finding tools can help analysts defeat many types of anti-analysis checks by proposing (and eventually forcing) program values to take a desired execution path through a program.

Developing path finding tools marks a shift for us to a new approach for binary static analysis rooted in constraint-based analysis using the Z3 Theorem Prover. We will describe our work through a series of blog posts as we continue to develop new features and tools using the constraint-based approach. In this first post I will highlight our strategies for addressing the path finding problem in Pharos.

Binary Path Finding

Finding a path to a given feature or place in a program is a common problem with a wide range of applications. Path analysis at the source code level is possible using a number of tools, such as symbolic executors. Unfortunately, source code is not always conveniently available. Closed-source libraries included in applications, third-party components, and legacy code are all examples of situations where source code may be missing. Naturally, malware rarely includes source code, which leaves analysts to study artifacts almost exclusively at the binary level.

Source code provides path finding tools a rich source of information, such as control flow conditions and data structure formats and names. Unfortunately, when programs are compiled into native executables, this information is often lost or optimized in ways that make it hard to recognize. Without this information, figuring out specific program paths can be extremely hard because analysts must reason through low-level implementation details, such as program stack management and function calling conventions.

To demonstrate the challenges presented at the binary level, let us first consider path finding in source code. In Listing 1 below, finding a path from line 1 to the target at line 19 of the function test() is relatively straightforward by visual inspection: we know that automatic integer variable x must be set to 42, which depends on automatic integer variable y being set to 2, which in turn depends on the three integer input parameters, i, j, and k being set to 6, 7, and 8 respectively. Required values aside, the control flow structures are relatively easy to reason through in source code because control flow conditions are straightforward.

Analyzing a path in a binary poses different types of challenges given the lack of defined data structures, compiler-generated optimizations, and loosely followed compilation conventions often found in executables. These challenges typically lead to dropping down to the assembly-code level and reverse engineering the program. Listing 2 below shows the disassembly for the test function as generated by popular disassembler IDA Pro. Note that the variables and easy-to-follow control flow structures are not nearly as clear in the disassembly, where automatic variables and parameters are accessed via stack memory locations, and decisions are combinations of conditional and unconditional jumps. Moreover, analysis only get harder as data structures get more complex.

The difficulty of following a path in a compiled program is clear when comparing the source code and binary control flow graphs (CFG). CFGs are directed graphs that show the structure of code representing the possible control flow transitions in the program. Both the source code and binary control flow graph for the test() function are shown in Figure 1.

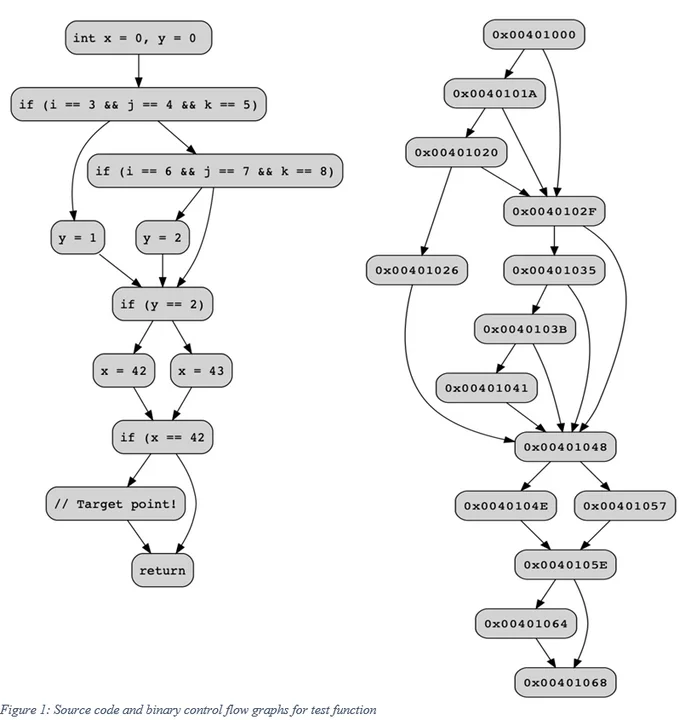
At the source-code level, each program statement (roughly) corresponds to a vertex in the CFG. At the binary level, each vertex corresponds to basic blocks. More and less detailed representations of a binary CFG are possible, but basic blocks are commonly used to show control flow. The overall shapes of these two CFGs are similar, but the compiled version includes additional vertices needed to implement conditional logic in assembly code.

Luckily, the Pharos Framework and ROSE compiler infrastructure provide many of the components necessary to reason about program paths in binaries. Pharos generates symbolic representations of common source code constructs at the binary level, which are suitable for analysis. In fact, Pharos creates symbolic values for both memory locations and registers, and these symbolic values show the impact of instructions on the program's state. Symbolic values are expressed as algebraic operations. For example, the access of the local variable x is done in assembly by referencing frame pointer variable [ebp-4]. Pharos represents this access as (add esp_0 -8) because it only uses the stack pointer for variable references, the ESP register rather than the frame pointer.) In Pharos, symbolic values are globally unique for the program and applied consistently for each operation.

Symbolic values provide a way to understand how data values flow through a program's CFG. In fact, the bulk of Pharos's initial setup is spent analyzing and propagating symbolic values in a program. One particularly useful symbolic value is the representation of the instruction pointer at any given location in the program. For example, in the binary CFG shown in Figure 1 the symbolic value of the instruction pointer at the conditional check at test() basic block address 0x00401000 is:

(ite (invert (zerop (add v5193 -3))) 0x0040102f 0x0040101a)

Although cryptic, when explained the control flow logic becomes clear. An ITE expression is an if-then-else expression, and the complete expression: ite condition true_expression false_expression will evaluate to true_expression if the condition is true, and false_expression otherwise. In the above example, the condition is whether the symbolic value v5193 is 3 (the strict translation is actually optimized as a test to see if adding -3 to symbolic value v5193 is 0). If this is so, then the instruction pointer advances to address 0x40102F, and otherwise to 0x40101A. This expression corresponds to the comparison of an input parameter to the value 3 and subsequent conditional jump.

ITE expressions are just one type of symbolic value included in Pharos and ROSE; there are many others available. The ROSE documentation contains a complete listing of symbolic operations and values. With a sense of control flow and symbolic program values, it is now possible to reason about the conditions under which certain paths will be taken in a binary.

PathAnalyzer: Generating and Solving Path Constraints

We have built a suite of tools, collectively referred to as PathAnalyzer, to reason about paths in a binary program. Our strategy is to encode the program as logical constraints and then let a constraint solver reason about viable paths. Specifically, we encode path segments and controlling values as Boolean expressions and then use a theorem prover to solve the constraints and propose a path.

We use the Z3 Theorem Prover to solve our constraints because it is efficient, open source, and supported by ROSE, and it includes advanced algorithms that we will discuss in future posts. The constraints themselves capture the control flow edges in the CFG, the conditions that control whether an edge is taken, and the values that control the condition. Listing 3 shows these three elements expressed in the SMT format of Z3.

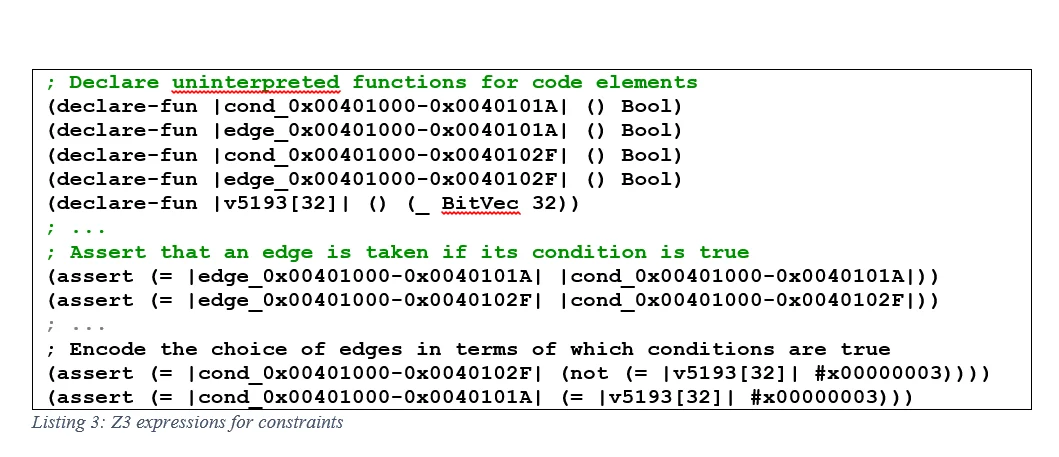
The constraints are arranged in such a way that the conditions controlling a decision are mutually exclusive. For example, in Listing 3 the assertion on line 9, cond_0x00401000-0x0040101A will be true if the symbolic value v5193 is 3, and the assertion on line 10, cond_0x00401000-0x0040102F will be true otherwise. Because the condition is controlled by a common value, both cannot be true simultaneously. In this example the label v5193 corresponds to the input parameter i, which is compared to 3. The other input parameter and automatic variables are encoded as Z3 assertions depending on how they influence code decisions. For the example program, we need input variable i = 6, j = 7, and k = 8 to set automatic variable y = 2, and finally x = 42.

When Z3 is provided these constraints, it attempts to determine if they are satisfiable, i.e. if a solution exists such that all the constraints are true. If they are, then Z3 generates a solution known as a model that includes assignments to each variable in the formula that will cause each assertion to be true. According to the official Z3 tutorial, models have a specific format:

(define-fun aVariable () [aType] [aValue])

where the value of aVariable is of type aType with value aValue. Going back to the example above, if the two conditions can be satisfied when they are evaluated by Z3, then a path to the target address of 0x00401064 is feasible. A portion of the model for the test() function is shown in Listing 4 for the choice between CFG edge 0x00401000-0x0040101A and CFG edge 0x00401000-0x0040102F. In this model, the variable that controls this decision, v5193 is set to 6, which satisfies the controlling condition that v5193 is not 3, thus edge_0x00401000-0x0040102F is true.

These values are then read back into Pharos and used to propose a path composed of two parts: the edges taken in the control flow graph and the values required to traverse those edges. In the portion of the model in Listing 4 the value v5139 is mapped to an input parameter i and assigned the value 6.

Much of the path analysis logic is in the core Pharos library. We are also working a new suite of on analyst tools that we are calling PathAnalyzer to generate and select viable paths between two basic blocks in a binary. The prototype tools that we are working on produce directed graphs in DOT format that include the necessary program data items (parameters and local variables) for a selected path between two points. An example of output produced by our prototype is shown in Figure 2. The green vertex represents the selected starting basic block, the red vertex indicates the goal basic block, and green edges in graph indicate the path selected.

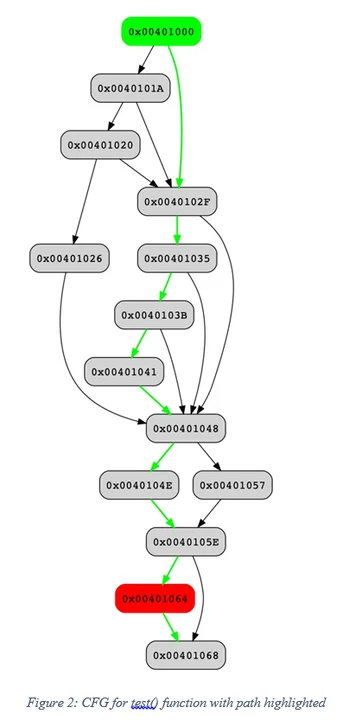
The values selected can then mapped back onto stack variables and input parameters tracked by Pharos:

Stack variables:

(add esp_0 -8) = 2

(add esp_0 -12) = 42

Input parameters:

0: (add esp_0 4) = 6

1: (add esp_0 8) = 7

2: (add esp_0 12) = 8

Taken together the annotated CFG and program values state that the path selected to reach address 0x00401064 from address 0x00401000 requires that the first stack variable at [esp-8] must be set to 2 and the input parameters must be 6, 7, and 8 in that order. In other words, calling the test function as test(6,7,8) will reach the desired target.

Looking Ahead

The path analysis we have described so far generates constraints from Pharos's symbolic representations, which have several limitations. First, Pharos's symbolic representations only represent the effects of loops up to a bounded number of iterations. If an analyst wants to find an execution that requires many executions of a, PathAnalyzer may incorrectly report that one does not exist. The other limitation is that Pharos's symbolic representation of memory is very simple and is primarily suitable for describing memory effects that are local to a function.

PathAnalyzer is generally unable to reason about executions with complicated inter-procedural memory behavior. The benefit of building on Pharos's symbolic representation, however, is that the constraints we generate are simplified and can generally be solved quickly. We are still exploring ways to balance the tradeoff between accuracy and performance and in future posts will discuss how we balance these competing concerns.

Our tools are continually evolving as we explore better ways to apply program analysis to reverse engineering and malware analysis problems, so keep an eye on our repository for updates. This post is just the tip of the iceberg of our work in path finding. In subsequent posts we will discuss how we approach other challenges, such as finding paths between multiple functions, and ultimately how we plan to use discovered paths to rewrite binaries so that when they are always executed.

Download Pharos Binary Analysis Framework and tools to support reverse engineering, which includes many new tools, improvements, and bug fixes.