Assuring information system security requires not just preventing system compromises but also finding adversaries already present in the network before they can attack from the inside. Defensive computer operations personnel have found the technique of cyber threat hunting a critical tool for identifying such threats. However, the time, expense, and expertise required for cyber threat hunting often inhibit the use of this approach. What’s needed is an autonomous cyber threat hunting tool that can run more pervasively, achieve standards of coverage currently considered impractical, and significantly reduce competition for limited time, dollars, and of course analyst resources. In this SEI blog post, I describe early work we’ve undertaken to apply game theory to the development of algorithms suitable for informing a fully autonomous threat hunting capability. As a starting point, we are developing what we refer to as chain games, a set of games in which threat hunting strategies can be evaluated and refined.

What is Threat Hunting?

The concept of threat hunting has been around for quite some time. In his seminal cybersecurity work, The Cuckoo’s Egg, Clifford Stoll described a threat hunt he conducted in 1986. However, threat hunting as a formal practice in security operations centers is a relatively recent development. It emerged as organizations began to appreciate how threat hunting complements two other common security activities: intrusion detection and incident response.

Intrusion detection tries to keep attackers from getting into the network and initiating an attack, whereas incident response seeks to mitigate damage done by an attacker after their attack has culminated. Threat hunting addresses the gap in the attack lifecycle in which an attacker has evaded initial detection and is planning or launching the initial stages of execution of their plan (see Figure 1). These attackers can do significant damage, but the risk hasn’t been fully realized yet by the victim organization. Threat hunting provides the defender another opportunity to find and neutralize attacks before that risk can materialize.

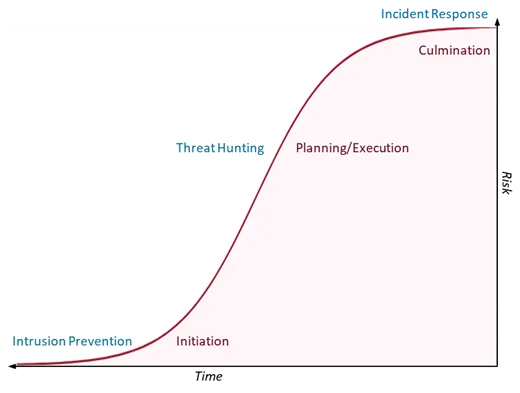
Threat hunting, however, requires a great deal of time and expertise. Individual hunts can take days or weeks, requiring hunt staff to make tough decisions about which datasets and systems to investigate and which to ignore. Every dataset they don’t investigate is one that could contain evidence of compromise.

The Vision: Autonomous Threat Hunting

Faster and larger-scale hunts could cover more data, better detect evidence of compromise, and alert defenders before the damage is done. These supercharged hunts could serve a reconnaissance function, giving human threat hunters information they can use to better direct their attention. To achieve this speed and economy of scale, however, requires automation. In fact, we believe it requires autonomy—the ability for automated processes to predicate, conduct, and conclude a threat hunt without human intervention.

Human-driven threat hunting is practiced throughout the DoD, but usually opportunistically when other activities, such as real-time analysis, permit. The expense of conducting threat hunt operations typically precludes thorough and comprehensive investigation of the area of regard. By not competing with real-time analysis or other activities for investigator effort, autonomous threat hunting could be run more pervasively and held to standards of coverage currently considered impractical.

At this early stage in our research on autonomous threat hunting, we’re focused in the short-term on quantitative evaluation, rapid strategic development, and capturing the adversarial quality of the threat hunting activity.

Modeling the Problem with Cyber Camouflage Games

At present, we remain a long way from our vision of a fully autonomous threat hunting capability that can investigate cybersecurity data at a scale approaching the one at which this data is created. To start down this path, we must be able to model the problem in an abstract way that we (and a future automated hunt system) can analyze. To do so, we needed to build an abstract framework in which we could rapidly prototype and test threat hunting strategies, possibly even programmatically using tools like machine learning. We believed a successful approach would reflect the idea that threat hunting involves both the attackers (who wish to hide in a network) and defenders (who want to find and evict them). These ideas led us to game theory.

We began by conducting a literature review of recent work in game theory to identify researchers already working in cybersecurity, ideally in ways we could immediately adapt to our purpose. Our review did indeed uncover recent work in the area of adversarial deception that we thought we could build on. Somewhat to our surprise, this body of work focused on how defenders could use deception, rather than attackers. In 2018, for example, a category of games was developed called cyber deception games. These games, contextualized in terms of the Cyber Kill Chain, sought to investigate the effectiveness of deception in frustrating attacker reconnaissance. Moreover, the cyber deception games were zero-sum games, meaning that the utility of the attacker and the defender balance out. We also found work on cyber camouflage games, which are similar to cyber deception games, but are general-sum games, meaning the attacker and defender utility are not directly related and can vary independently.

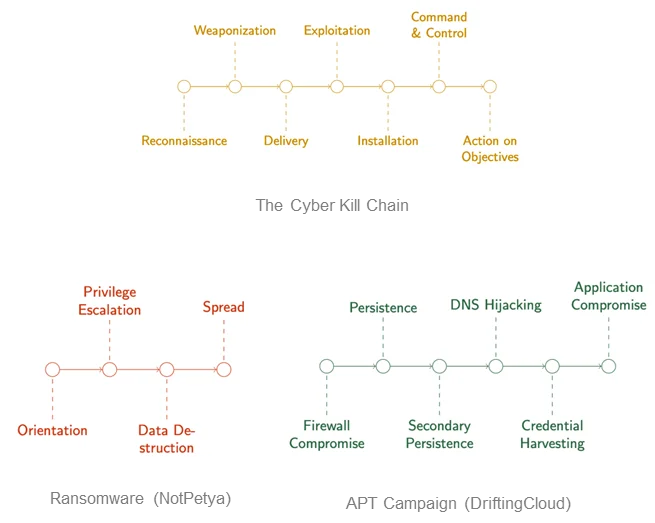
Seeing game theory applied to real cybersecurity problems made us confident we could apply it to threat hunting. The most influential part of this work on our research concerns the Cyber Kill Chain. Kill chains are a concept derived from kinetic warfare, and they are usually used in operational cybersecurity as a communication and categorization tool. Kill chains are often used to break down patterns of attack, such as in ransomware and other malware. A better way to think of these chains is as attack chains, because they’re being used for attack characterization.

Elsewhere in cybersecurity, analysis is done using attack graphs, which map all the paths by which a system might be compromised (see Figure 2). You can think of this kind of graph as a composition of individual attack chains. Consequently, while the work on cyber deception games mainly used references to the Cyber Kill Chain to contextualize the work, it struck us as a powerful formalism that we could orient our model around.

In the following sections, I’ll describe that model and walk you through some simple examples, describe our current work, and highlight the work we plan to undertake in the near future.

Simple Chain Games

Our approach to modeling cyber threat hunting employs a family of games we refer to as chain games, because they’re oriented around a very abstract model of the kill chains. We call this abstract model a state chain. Each state in a chain represents a position of advantage in a network, a computer, a cloud application, or a number of other different contexts in an enterprise’s information system infrastructure. Chain games are played on state chains. States represent positions in the network conveying advantage (or disadvantage) to the attacker. The utility and cost of occupying a state can be quantified. Progress through the state chain motivates the attacker; stopping progress motivates the defender.

You can think of an attacker initially establishing themselves in one state—“state zero” (see “S0” in Figure 3). Perhaps someone in the organization clicked on a malicious link or an email attachment. The attacker’s first order of business is to establish persistence on the machine they’ve infected to ward against being accidentally evicted. To establish this persistence, the attacker writes a file to disk and makes sure it’s executed when the machine starts up. In so doing, they’ve moved from initial infection to persistence, and they’re advancing into state one. Each additional step an attacker takes to further their goals advances them into another state.

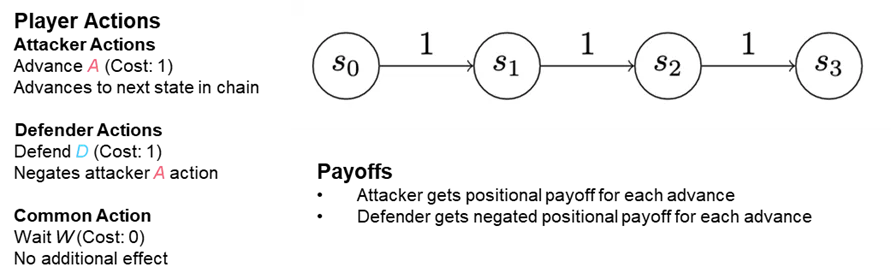
The field isn’t wide open for an attacker to take these actions. For instance, if they’re not a privileged user, they might not be able to set their file to execute. What’s more, trying to do so will reveal their presence to an endpoint security solution. So, they’ll need to try to elevate their privileges and become an admin user. However, that move could also arouse suspicion. Both activities entail some risk, but they also have a potential reward.

To model this situation, a cost is imposed any time an attacker wants to advance down the chain, but the attacker could alternatively earn a benefit by successfully moving into a given state. The defender does not travel along the chain like the attacker: The defender is somewhere in the network, able to observe (and sometimes stop) some of the attacker's moves.

All of these chain games are two-player games played between an attacker and a defender, and they all follow rules governing how the attacker advances through the chain and how the defender might try to stop them. The games are confined to a fixed number of turns, usually two or three in these examples, and are mostly general-sum games: each player gains and loses utility independently. We conceived these games as simultaneous turn games: Both players decide what to do at the same time and those actions are resolved simultaneously.

We can also apply graphs to track the play (see Figure 4). From the attacker standpoint, this graph represents a choice they can make about how to attack, exploit, or otherwise operate within the defender network. Once the attacker makes that choice, we can think of the path the attacker chooses as a chain. So even though the analysis is oriented around chains, there are ways we can treat more complex graphs to think of them like chains.

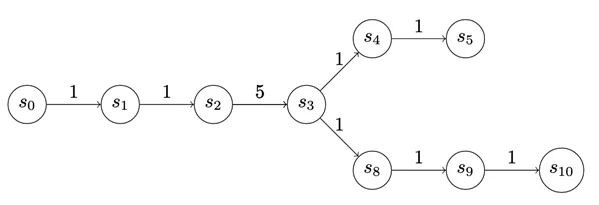
The payoff to enter a state is depicted at the edges of the graphs in Figure 5. The payoff doesn’t have to be the same for each state. We use uniform-value chains for the first few examples, but there’s actually a lot of expressiveness in this cost assignment. For instance, in the chain below, S3 may represent a valuable source of information, but to access it the attacker may have to take on some net risk.

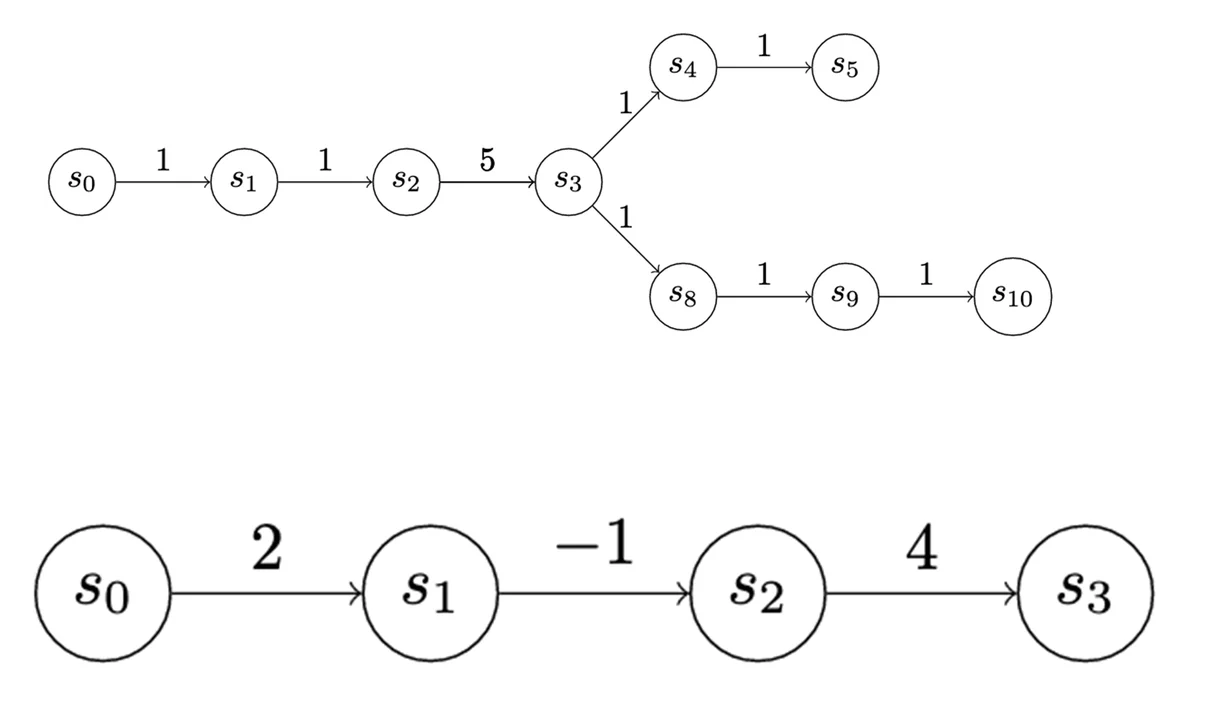
In the first game, which is a very simple game we can call “Version 0,” the attacker and defender have two actions each (Figure 6). The attacker can advance, meaning they can go from whatever state they’re in to the next state, collecting the utility for entering the state and paying the cost to advance. In this case, the utility for each advance is 1, which is fully offset by the cost.

However, the defender receives -1 utility whenever an attacker advances (zero-sum). This scoring isn’t meant to incentivize the attacker to advance so much as to motivate the defender to exercise their detect action. A detect will stop an advance, meaning the attacker pays the cost for the advance but doesn’t change states and doesn’t get any additional utility. However, exercising the detect action costs the defender 1 utility. Consequently, because a penalty is imposed when the attacker advances, the defender is motivated to pay the cost for their detect action and avoid being punished for an attacker advance. Finally, both the attacker and the defender can choose to wait. Waiting costs nothing, and earns nothing.

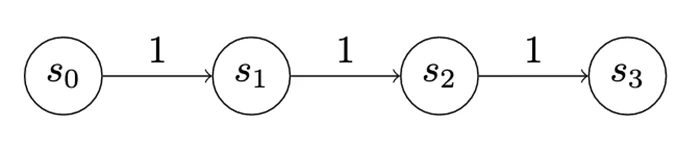
Figure 7 illustrates the payoff matrix of a Version 0 game. The matrix shows the total net utility for each player when they play the game for a set number of turns (in this case, two turns). Each row represents the defender choosing a single sequence of actions: The first row shows what happens when the defender waits for two turns across all the other different sequences of actions the attacker can take. Each cell is a pair of numbers that shows how well that works out for the defender, which is the left number, and the attacker on the right.

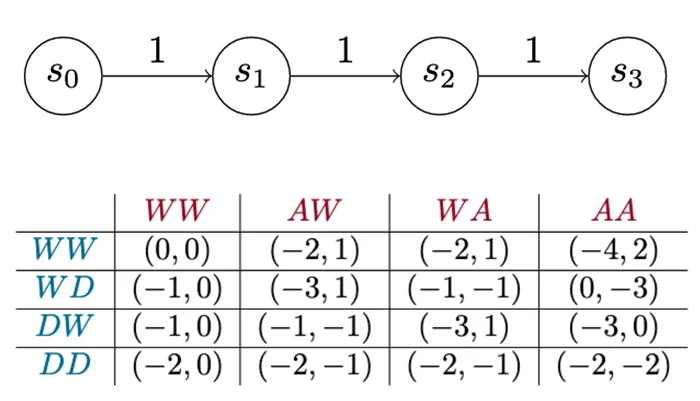
This matrix shows every strategy the attacker or the defender can employ in this game over two turns. Technically, it shows every pure strategy. With that information, we can perform other kinds of analysis, such as identifying dominant strategies. In this case, it turns out there is one dominant strategy each for the attacker and the defender. The attacker’s dominant strategy is to always try to advance. The defender’s dominant strategy is, “Never detect!” In other words, always wait. Intuitively, it seems that the -1 utility penalty assessed to an attacker to advance isn’t enough to make it worthwhile for the defender to pay the cost to detect. So, think of this version of the game as a teaching tool. A big part of making this approach work lies in choosing good values for these costs and payouts.

Introducing Camouflage

In a second version of our simple chain game, we introduced some mechanics that helped us think about when to deploy and detect attacker camouflage. You’ll recall from our literature review that prior work on cyber camouflage games and cyber deception games modeled deception as defensive activities, but here it’s a property of the attacker.

This game is identical to Version 0, except each player’s primary action has been split in two. Instead of a single advance action, the attacker has a noisy advance action and a camouflaged advance action. Consequently, this version reflects tendencies we see in actual cyber attacks: Some attackers try to remove evidence of their activity or choose methods that may be less reliable but harder to detect. Others move boldly forward. In this game, that dynamic is represented by making a camouflaged advance more costly than a noisy advance, but it’s harder to detect.

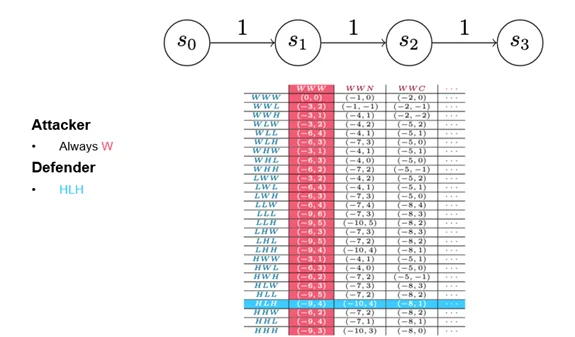
On the defender side, the detect action now splits into a weak detect and a strong detect. A weak detect can only stop noisy advances; a strong detect can stop both types of attacker advance, but–of course–it costs more. In the payout matrix (Figure 8), weak and strong detects are referred to as low and high detections. (Figure 8 presents the full payout matrix. I don’t expect you to be able to read it, but I wanted to provide a sense of how quickly simple changes can complicate analysis.)

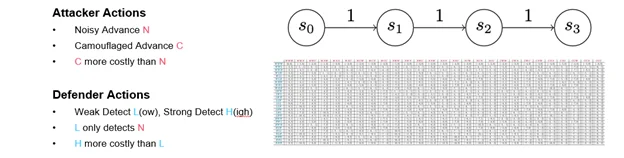
Dominant Strategy

In game theory, a dominant strategy is not the one that always wins; rather, a strategy is deemed dominant if its performance is the best you can expect against a perfectly rational opponent. Figure 9 provides a detail of the payout matrix that shows all the defender strategies and three of the attacker strategies. Despite the addition of a camouflaged action, the game still produces one dominant strategy each for both the attacker and the defender. We’ve tuned the game, however, so that the attacker should never advance, which is an artifact of the way we’ve chosen to structure the costs and payouts. So, while these particular strategies reflect the way the game is tuned, we might find that attackers in real life deploy strategies other than the optimal rational strategy. If they do, we might want to adjust our behavior to optimize for that situation.

More Complex Chains

The two games I’ve discussed thus far were played on chains with uniform advancement costs. When we vary that assumption, we start to get much more interesting results. For instance, a three-state chain (Figure 10) is a very reasonable characterization of certain types of attack: An attacker gets a lot of utility out of the initial infection, and sees a lot of value in taking a particular action on objectives, but getting into position to take that action may incur little, no, or even negative utility.

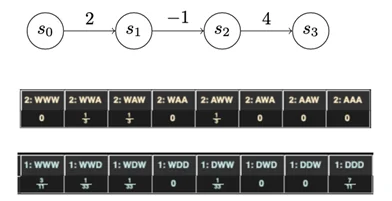
Introducing chains with complex utilities yields much more complex strategies for both attacker and defender. Figure 10 is derived from the output of Gambit, which is a game analysis tool, that describes the dominant strategies for a game played over the chain shown below. The dominant strategies are now mixed strategies. A mixed strategy means that there is no “right strategy” for any single playthrough; you can only define optimal play in terms of probabilities. For instance, the attacker here should always advance one turn and wait the other two turns. However, the attacker should mix it up when they make their advance, spreading them out equally among all three turns.

This payout structure may reflect, for instance, the implementation of a mitigation of some sort in front of a valuable asset. The attacker is deterred from attacking the asset by the mitigation. But they’re also getting some utility from making that first advance. If that utility were smaller, for instance because the utility of compromising another part of the network was mitigated, perhaps it would be rational for the attacker to either try to advance all the way down the chain or never try to advance at all. Clearly, more work is needed here to better understand what’s going on, but we’re encouraged by seeing this more complex behavior emerge from such a simple change.

Future Work

Our early efforts in this line of research on automated threat hunting have suggested three areas of future work:

• enriching the game space
• simulation
• mapping to the problem domain

We discuss each of these areas below.

Enriching the Game Space to Resemble a Threat Hunt

Threat hunting usually happens as a set of data queries to uncover evidence of compromise. We can reflect this action in our game by introducing an information vector. The information vector changes when the attacker advances, but not all the information in the vector is automatically available (and therefore invisible) to the defender. For instance, as the attacker advances from S0 to S1 (Figure 11), there is no change in the information the defender has access to. Advancing from S1 to S2 changes some of the defender-visible data, however, enabling them to detect attacker activity.

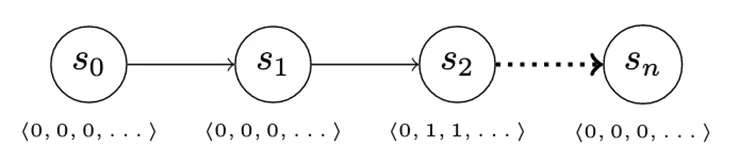
The addition of the information vector permits a number of interesting enhancements to our simple game. Deception can be modeled as multiple advance actions that differ in the parts of the information vector that they modify. Similarly, the defender’s detect actions can collect evidence from different parts of the vector, or perhaps unlock parts of the vector to which the defender normally has no access. This behavior may reflect applying enhanced logging to processes or systems where compromise may be suspected, for instance.

Finally, we can further defender actions by introducing actions to remediate an attacker presence; for example, by suggesting a host be reinstalled, or by ordering configuration changes to a resource that make it more difficult for the attacker to advance into.

Simulation

As shown in the earlier example games, small complications can result in many more options for player behavior, and this effect creates a larger space in which to conduct analysis. Simulation can provide approximate useful information about questions that are computationally infeasible to answer exhaustively. Simulation also allows us to model situations in which theoretical assumptions are violated to determine whether some theoretically suboptimal strategies have better performance in specific conditions.

Figure 12 presents the definition of version 0 of our game in OpenSpiel, a simulation framework from DeepMind. We plan to use this tool for more active experimentation in the coming year.

Mapping the Model to the Problem of Threat Hunting

Our last example game illustrated how we can use different advance costs on state chains to better reflect patterns of network protection and patterns of attacker behavior. These patterns vary depending on how we choose to interpret the relationship of the state chain to the attacking player. More complexity here results in a much richer set of strategies than the uniform-value chains do.

There are other ways we can map primitives in our games to more aspects of the real-world threat hunting problem. We can use simulation to model empirically observed strategies, and we can map features in the information vector to information elements present in real-world systems. This exercise lies at the heart of the work we plan to do in the near future.

Conclusion

Manual threat hunting techniques currently available are expensive, time consuming, resource intensive, and dependent on expertise. Faster, less expensive, and less resource-intensive threat hunting techniques would help organizations investigate more data sources, coordinate for coverage, and help triage human threat hunts. The key to faster, less expensive threat hunting is autonomy. To develop effective autonomous threat hunting techniques, we are developing chain games, which are a set of games we use to evaluate threat hunting strategies. In the near term, our goals are modeling, quantitatively evaluating and developing strategies, rapid strategic development, and capturing the adversarial quality of threat hunting activity. In the long term, our goal is an autonomous threat hunting tool that can predict adversarial activity, investigate it, and draw conclusions to inform human analysts.