The Promise of Deep Learning on Graphs
PUBLISHED IN
Artificial Intelligence EngineeringA growing number of Department of Defense (DoD) data problems are graph problems: the data from sources such as sensor feeds, web traffic, and supply chains are full of irregular relationships that require graphs to represent explicitly and mathematically. For example, modern test and evaluation produces massive, heterogeneous datasets, and analysts can use graphs to reveal otherwise hidden patterns in these data, affording the DoD a far more complete understanding of a system's effectiveness, survivability, and safety. But such datasets are growing increasingly large and increasingly complex, demanding new approaches for proper analysis. Machine learning seems to recommend itself to such datasets, but conventional machine learning approaches to graph problems are sharply limited.
Deep learning is the current ne plus ultra for big data problems, using brain-inspired algorithms to 'learn' from massive amounts of data and outperform conventional optimization and decision systems. Deep learning, however, hasn't been meaningfully extended beyond Euclidean data. Attempts to generalize deep learning to non-Euclidean domains have been dubbed geometric deep learning by the machine learning community.
Convolutional neural networks (CNNs) in particular have transformed image processing and computer vision in just a few short years. This blog post details a new research effort by the SEI and Carnegie Mellon University's Electrical and Computer Engineering department to apply graph signal processing formalisms in the creation of new deep learning tools for graph convolutional neural networks (GCNNs), so that the same techniques that have revolutionized computer vision can be applied to graph problems.
The Importance and Difficulty of Processing Graph Data
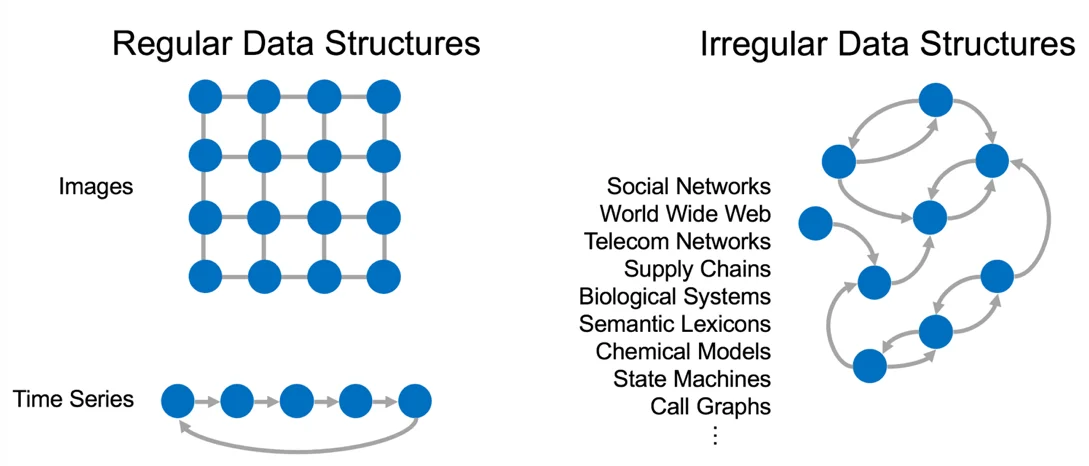
Fig. 1: Regular data structures vs. irregular data structures
If machine learning techniques could be successfully extended to irregular data structures represented by graphs, they could be applied to a much wider world of important data domains, as shown in Fig. 1. Use cases include inductive learning, semantic labeling, webpage ranking and taxonomy, community detection, recommendation system, network analysis, logistics monitoring, and 3D action recognition. DARPA's Hierarchical Identify Verify Exploit (HIVE) program specifically cites three important problem domains of note: cybersecurity, social media analysis, and infrastructure monitoring.
The theory and engineering tools for working on regular data structures are quite mature--operations such as filtering, denoising, and compression are well understood. But when it comes to irregular structures, like that depicted on the right in Fig. 1, analyzing the data on such structures lacks the same kind of methodological rigor.
Conventional machine learning approaches to graphs typically neither generalize well (i.e., working only on a subset of graph topologies), nor model reality well (e.g., making Euclidean assumptions where no such behavior exists). Such approaches are further limited by poor scaling, an increasingly dire restriction in an age of superabundant data. Early work has been done to extend CNNs to graph problems, but, until recently, these approaches have been brittle and computationally expensive.
Our Approach
Topology-adaptive graph convolutional networks, first introduced in 2017 by researchers at CMU, are computationally cheaper, are empirically more accurate, and work independent of graph topology. Whereas current GCNN models require computationally expensive spectral decomposition or use Chebyshev polynomials that degrade accuracy, this new class of GCNNs is grounded in graph signal processing theory. Graph signal processing unifies the vertex and spectral domains; by this approach GCNNs can be applied to any graph topology without the limiting assumptions and approximations of other methods.
Despite this advance, there is still an innovation gap: CNNs, and deep learners in general, are currently implemented with a suite of tools that require both engineering and further research to extend to graph domains. These tools allow for deeper, more robust network architectures, which in turn improve accuracy and generalization, as well as ease implementation. We are researching techniques at the juncture of theory and practice, like pooling, sampling, dropout, and zero-padding. We are also studying learning over directed graphs, and using new tools like PyTorch Geometric to build ready implementations.
We are interested in two classes of graph learning problems:
- Predicting information about unlabeled nodes in a graph, based on labeled nodes. Performing this kind of learning, sometimes called transductive learning or semi-supervised learning, on citation networks (e.g., Citeseer) has become a standard test in the research community.
- Predicting information about new graphs, based on labeled graphs. We will be performing this kind of learning, sometimes called inductive or supervised learning, on datasets like traffic data--wherein each graph corresponds to a traffic pattern on a grid of intersections--and protein-protein interactions--wherein each graph corresponds to a different human tissue.
We intend to bridge the innovation gap between fundamental advances in the theory of GCNNs and their widespread, practical implementation for mission problems. At the conclusion of this project we will publish our results and host open source code.
Looking Ahead
Scalable GCNN implementations will be a potent tool for learning on graphs. The motivating conceit of machine learning--solving problems with data instead of explicit formulae--only grows in power and appeal with the growth of data. Yet DoD data are growing not just in size, but in heterogeneity. Navigating that irregularity and complexity, and doing so at scale, is vital, and geometric deep learning opens a path.
Additional Resources
Read the SEI Blog Post Developing a Software Library for Graph Analytics.
public int test(){
return 1;
}
More In Artificial Intelligence Engineering
PUBLISHED IN
Artificial Intelligence EngineeringGet updates on our latest work.
Sign up to have the latest post sent to your inbox weekly.
Subscribe Get our RSS feedMore In Artificial Intelligence Engineering
Get updates on our latest work.
Each week, our researchers write about the latest in software engineering, cybersecurity and artificial intelligence. Sign up to get the latest post sent to your inbox the day it's published.
Subscribe Get our RSS feed
