Practical Math for Your Security Operations - Part 1 of 3
Hi, this is Vijay Sarvepalli, Security Solutions Engineer in the CERT Division. Mathematics is part of your daily tasks if you're a security analyst. In this blog post series, I'll explore some practical uses of math in your SOC (Security Operations Center). This pragmatic approach will hopefully help enhance your use of mathematics for network security.
Part 1: Set Theory, Venn Diagram and IP Addresses
Today's SOC operations are driven by feeds of indicators that are consumed by various processes to provide ongoing security monitoring. Some good examples of these indicators are lists or sets (i.e., unique lists of items) of IP addresses, domain names, URLs (Uniform Resource Links), and file signatures (e.g., MD-5). It is a very common operation to look for the presence or absence of these indicators in logs, netflow (network flow), and IDS (Intrusion Detection Sensor) alerts. Most of these operations are simple set operations that can be explained using Venn diagrams and can be achieved using some tools. Set operations can also be effective in comparing today's data to yesterday's data or data from last week or last month to derive differences. These operations translate to new devices observed on the network.
Example 1: Set Intersection
Lets start with a simple example the task is to find IP addresses that were observed in two different sets. This is basically a set intersect operation; you can see this in the following Venn diagram.
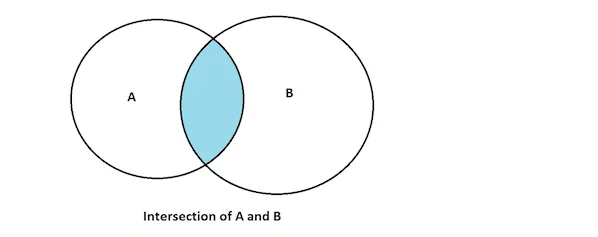
In this first example, we want to use network profiling to find the IP addresses of remote systems that communicate with our servers on weekends and weekdays. The source is two sets of external IP addresses:
Set A - - A set that successfully communicated with our server network over weekends S-Su
Set B - - A set that successfully communicated with our server network over weekdays M-F
Here is an example dataset for this analysis:
| Set A | Set B |
|---|---|
| 10.11.11.1 | 172.17.12.1 |
| 192.168.31.11 | 10.11.11.1 |
| 172.16.44.1 | 10.253.11.1 |
| 10.253.11.1 | 10.0.0.11 |
| 10.131.11.19 | 192.168.23.23 |
| 10.144.244.233 |
Here is an example statement to perform the intersect operation using the SiLK tool rwsettool:
[bash]$ rwsettool --intersect seta.set setb.set | rwsetcat
10.11.11.1
10.253.11.1The files seta.set and setb.set are IPSet files that contain the above data in the table above.
Here is an example statement to perform the same operation using SQL:
sqlite> SELECT A.IP FROM IPSETA A INNER JOIN IPSETB B ON A.IP=B.IP;
"10.11.11.1"
"10.253.11.1"Example 2: Relative Component or Set-Theoretic Difference
Suppose you want to analyze external IP addresses that communicate with your server only on the weekends. This operation uses a a set of elements in B, but not in A. In set theory, this operation is called a "relative complement" or "set-theoretic difference" operation.
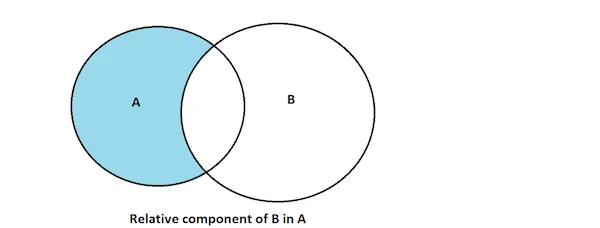
Here is an example statement to perform the relative complement of B in A using the NetSA-developed SiLK tool suite:
[bash]$ rwsettool --difference seta.set setb.set | rwsetcat
10.131.11.19
172.16.44.1
192.168.31.11Here is an example statement to perform the same operation using SQL:
sql> SELECT A.IP FROM IPSETA A LEFT OUTER JOIN IPSETB B ON A.IP=B.IP WHERE B.IP is null; "192.168.31.11"
"172.16.44.1"
"10.131.11.19"Example 3: Symmetric Difference of Set A and B
In this use case, the objective is to find IP addresses that communicated with us only on weekdays or weekends but not on both. This operation is called "symmetric difference" in set theory.
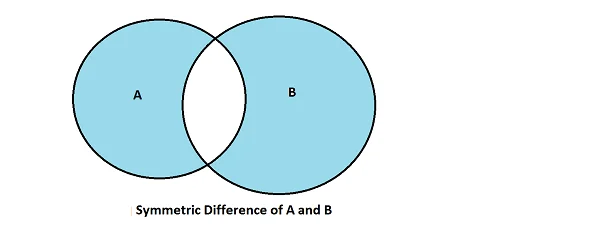
Using the SiLK tool suite, this task is a two-step operation: find the union of both sets and then subtract the intersection:
[bash]$ rwsettool --union seta.set setb.set > setab.set
[bash]$ rwsettool --intersect seta.set setb.set | rwsettool --difference setab.set stdin | rwsetcat
10.0.0.11
10.131.11.19
10.144.244.233
172.16.44.1
172.17.12.1
192.168.23.23
192.168.31.11The same operation in SQL depends on the software. Some database software, such as Postgres, Microsoft SQL, and Oracle, support full outer join, but others do not (e.g., Sqlite and MySQL). Here is the same operation using full outer join:
SQL> select a.ip,b.ip from ipsetb b full outer join ipseta a on a.ip=b.ip where a.ip is null or b.ip is null;
IP IP
--------------- ---------------
172.17.12.1
10.0.0.11
192.168.23.23
10.144.244.233
10.131.11.19
172.16.44.1
192.168.31.11Other Operations
All basic set operations can be related to these types of use cases and can be achieved using standard data processing and analysis tools available in your SOC. In the next blog entry, I'll explore a little bit on more advanced math topics such as statistics and probability.
The table below summarizes common set operations and how they are performed using tools in your SOC:
| Set Theory terminology | SiLK tools suite | SQL operation |
|---|---|---|
| Intersection(A ∩ B) | rwsettool --intersect | INNER JOIN |
| Relative complement(Ac ∩ B) or (A \ B) | rwsettool --difference | (LEFT OUTER JOIN) EXCEPT(INNER JOIN) |
| Symmetric difference(A \ B) ∪ (B \ A) | rwsettool --difference (rwsettool --union)(rwsettool --intersect) | (FULL OUTER JOIN) EXCEPT(INNER JOIN) |
Conclusion
Using mathematics in your SOC can be an effective way to either look for information in your log data or find anomalies in network data. In this series of blog posts, I'll explore other topics, such as statistics and probability theory, and conclude with advanced topics, such as Algebra and Number Theory, that can be applied in simple and effective ways for security operations.
If you have questions or suggestions, contact the NetSA team via email at netsa-contact@cert.org.
More By The Authors
More In CERT/CC Vulnerabilities
PUBLISHED IN
Get updates on our latest work.
Sign up to have the latest post sent to your inbox weekly.
Subscribe Get our RSS feedMore In CERT/CC Vulnerabilities
Get updates on our latest work.
Each week, our researchers write about the latest in software engineering, cybersecurity and artificial intelligence. Sign up to get the latest post sent to your inbox the day it's published.
Subscribe Get our RSS feed
