Practical Math for Your Security Operations - Part 3 of 3
Hi, this is Vijay Sarvepalli, security solutions engineer in the CERT Division again. In the earlier blog entries for this series, I introduced set theory and standard deviation. This blog entry is about entropy, a physics principle that has made its way into many mathematical applications. Entropy has been applied in many informational science topics. In this blog post, I introduce a way to use entropy to detect anomalies in network communications patterns.
Entropy in Network Flow Data
Entropy is defined as a "measure of disorder." In information theory, entropy is usually used to measure uncertainty in a random variable. In this example, however, I use entropy to differentiate network behavior. While analyzing network data, our security analyst Geoff Sanders found that the lack of entropy in network communications patterns between two machines indicates reliable communications channels. These channels can be communications classified as NTP (Network Time Protocol), streaming (audio, video), or channeling of other types (beaconing, command and control used by malware/malicious software).
The number of bytes transferred over time is used in this example to measure this type of distribution in communications. Once a communications channel is established (such as a TCP session), packets transfer bytes of data over this channel. If we measure entropy using the number of bytes per packet transferred over this channel, a larger entropy value shows more variety of data sizes being transferred. A smaller entropy value indicates a steady communications channel sending the same amount of data in a repeated fashion.
For communications with typical website and distributed content providers, such as Google and Amazon, a large entropy is identified by measuring this type of network communications entropy value. To better illustrate this type of entropy, let's walk through an example.
A simple python function calculates the Shannon entropy. Since we are not really concerned about random variables, the simple Shannon entropy is used. The equation for calculating the Shannon entropy is
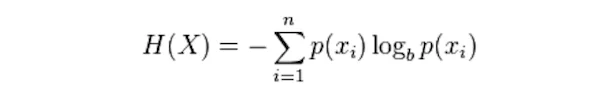
def Hentropy(*args):
""" Find the Shannon entropy of an arguments list """
xi = zip(*args)
prob = [ float(xi.count(c)) / len(xi) for c in dict.fromkeys(list(xi)) ]
H = - sum([ p * math.log(p,2) for p in prob ])
return H
This function assumes you are sending value integers or normalized floating-point numbers at the same precision. The bytes per packet in this example has beeen normalized to 2 digits floating point number (%.2f).
Using this entropy of number of bytes per packet transferred over time bins, you can find some network communications anomalies that lead to the investigation of possibly compromised systems on the network. The table below provides an example output of such analysis. A reasonable number of samples should be used when calculating these values. In this example, I used 200 network flow samples to calculate entropy values.
| Source IP | Destination IP | Duration (seconds) | Entropy (Bytes/Time) |
| 10.31.11.19 | 207.152.125.173 | 16500 | 4.7136 |
| 10.11.10.29 | 69.28.187.66 | 19800 | 4.6144 |
| 192.168.33.11 | 50.116.98.50 | 23500 | 4.3111 |
| 192.168.21.11 | 10.10.10.11(*) | 23430 | 0.1534 |
* IP address modified.
An important step in selecting network flow data for analysis is choosing the type of network traffic. In the example, network traffic was chosen using two criteria:
i. Length of communications (> 20 minutes)
ii. Number of flow samples (>= 200 samples)
Analyzing this traffic reveals that the first three entries show communications with major CDN (Content Delivery Network - Akamai, Limelight, and Amazon) providers. The communications with CDN providers shows a fairly random amount of data being transferred over established network communications channels.
These communications indicate small images, icons, and text being transferred between the client and the server. The last row in the communications indicates a long session that lasted 23,430 seconds (over 6 hours) but shows no change in its communications pattern. This session could be malware beaconing back to "phone home" to a command and control server. Further analysis can help identify the source system for a potential malware infection. In this case, it was confirmed as an infected system.
Conclusion
Using mathematics can be an effective tool to use in your SOC to either parse a large amount of network data or to find anomalies in data. Below are more examples of mathematical approaches that can be used in a practical way for your security operations:
Algebraic Geometry. Geospatial analysis of IP geolocation data is a mathematical approach that can be used, for example, to build a heat map that helps to visualize the geospatial distribution of data. Readily reusable software is available to implement algebraic geometry in your security operations.
Probability Theory. Bloom filtering quickly detects negative hits while searching large datasets of whitelists, such as domain names and URLs. Bloom filters help to define a "hash" index that represents a large dataset. Thus, it is a space efficient way to check if an element exists in a set.
Number Theory. Modulus arithmetic is a great way to build indexes of large structured datasets, such as IPV4 and IPV6 addresses. Modulus-based indices are effective for quick search and can also be used to abstract joins between two datasets. Thus, instead of comparing two large datasets, a quick intersection between modulus-based indices of these datasets can significantly cut down the amount of data that must be compared.
I hope this blog post helps you to use math effectively in your security operations center data analysis tasks. If you have any questions, contact us via email at netsa-contact@cert.org.
More By The Author
More In CERT/CC Vulnerabilities
PUBLISHED IN
Get updates on our latest work.
Sign up to have the latest post sent to your inbox weekly.
Subscribe Get our RSS feedMore In CERT/CC Vulnerabilities
Get updates on our latest work.
Each week, our researchers write about the latest in software engineering, cybersecurity and artificial intelligence. Sign up to get the latest post sent to your inbox the day it's published.
Subscribe Get our RSS feed
